Derivada

Al final del cuaderno anterior vimos que las razones de cambio instantáneas tienen importantes aplicaciones en el ámbito de la administración, en este cuaderno abordaremos la forma gelométrica de ésta razón de cambio (pendiente de la recta tangente) y estudiaremos las propiedades de la derivada.

Interpretación gráfica de la derivada

Como vimos en las clases anteriores, la razon de cambio nos permite determinar la pendiente de la recta tangente de una función $f(x)$ en un punto $x_0$.

from sympy import *
x=symbols('x')
f=(x**2)
df =diff(f)
m=df.subs(x,1)
rt=m*(x-1)+1
G=plot(f,(x,-0.5,3),axis_center=(0,0),ylim=(0,3),line_color='g',show=false)
G.extend(plot(rt,(x,-0.5,3),line_color='r',show=false))
G.show()

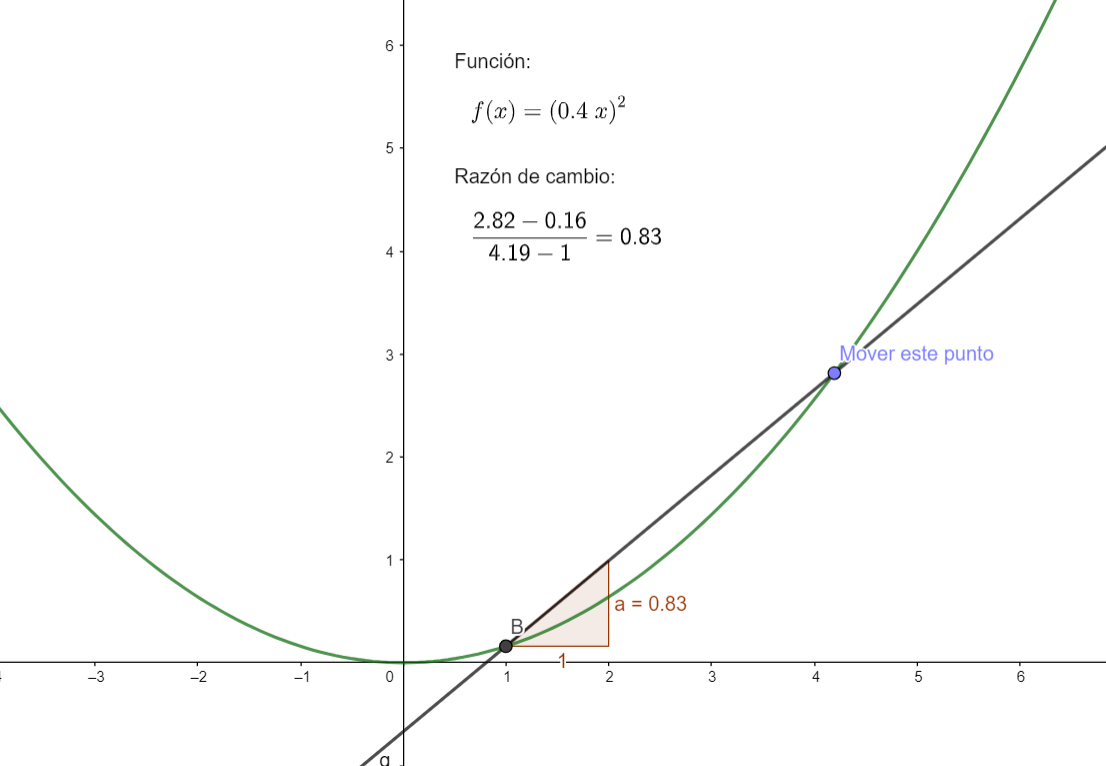
Visualización de la razón de cambio instantánea

A continuación vemos una pequeña animación de Geogebra que justifica el uso de la derivada, clickea sobre la imagen:

Derivada

como vimos anteriormente, la derivada de una función $f$ se define como la razón de cambio en el intervalo $[x,x+h]$ cuando $h$ tiende a cero, es decir $$f'(h)=\lim_{x\to0}\frac{f(x+h)-f(x)}{h}$$

Reglas de derivación

Con los ejemplos que se han desarrollado hasta el momento, es claro que el cálculo de las derivadas mediante la definición puede llegar a ser un poco egorroso y desgastante, para ahorrar un poco de esfuerzos las reglas de derivación son muy eficientes.

$f(x)$	$f'(x)$
$k$	$0$
$(u)^n$	$n(u)^{n-1}(u')$
$e^u$	$e^u(u')$
$ln(u)$	$\frac{1}{u}(u')$
$f(x)\pm g(x)$	$f'(x)\pm g'(x)$

Ejemplos:

1. Halle la derivada de la función $f(x)=(2x-1)^3$. #### Solución: Claramente se pide hallar la derivada de algo del estilo $(u)^n$ junto con la regla de de la suma/resta, de modo que su derivada será

$$f'(x)=3(2x+1)^{3-1}(2)=3(2x+1)^{2}(2).$$

1. Halle la derivada de $y=e^{7x^2-10x}$. #### Solución: En este ejemplo deben emplearse la tercera regla de derivación que se puede observar en la tabla como también la regla de la suma/resta, por lo tanto $$y'=e^{7x^2-10x}\left( 2\left(7x^{2-1}\right)-10\right)=e^{7x^2-10x}\left( 14x-10\right).$$

2. Calcule la derivada de $g(t)=ln(5t^4-3)$. #### Solución: Para desarrollar el ejercicio se deben utilizar la cuarta regla de la tabla y la de la suma/resta, por lo que $$g'(t)=\frac{1}{5t^4-3}\left(5\left(4t^{4-1}\right)\right)=\frac{20t^3}{5t^4-3}.$$

Derivadas en Python usando sympy

Usando el paquete sympy usamos la función diff() para calcular la derivada de una función.

Sintáxis de la función diff:

diff(función,variable)

En las siguientes líneas calculamos la derivada de las funciones de los ejemplos anteriores:

x=symbols('x') #Recuerda definir el simbolo x para que la máquina reconozca que x es una variable.

L1=(2*x-1)**3
L1 #Veamos la función

$\displaystyle \left(2 x - 1\right)^{3}$

diff(L1) #diff calcula la derivada

$\displaystyle 6 \left(2 x - 1\right)^{2}$

expand(diff(L1)) #expand permite expandir la función

$\displaystyle 24 x^{2} - 24 x + 6$

L2= E**(7*x**2-10*x)
L2

$\displaystyle e^{7 x^{2} - 10 x}$

diff(L2)

$\displaystyle \left(14 x - 10\right) e^{7 x^{2} - 10 x}$

expand(diff(L2))

$\displaystyle 14 x e^{- 10 x} e^{7 x^{2}} - 10 e^{- 10 x} e^{7 x^{2}}$

Regla del producto

$$\left(f(x)g(x)\right)'=f'(x)g(x)+g'(x)f(x)$$

Esta regla es muy importante ya que no siempre se tiene funciones que contengan un único factor, por ejemplo $$h(x)=(4x-5)^3e^x$$ su derivada será $$h'(x)=3(4x-5)^2(4)e^x+e^x(1)(4x-5)^3$$

En lo que sigue encontrará un algoritmo muy sencillo que calcula la derivada del producto y muestra el razonamiento a realizar.

def derivaciondeproducto(f):
    print("Identifique dos posibles factores de") 
    pprint(f,use_unicode=False) 
    
    f1=input("Ingrese el primer factor: ")
    f1=sympify(f1)
    f2=input("Ingrese el segundo factor: ")
    f2=sympify(f2)
    if simplify(f1*f2)==simplify(f):
        print("Muy bien. El calculo de la derivada se hace de la siguiente manera:")
        pprint(diff(f1)*f2+diff(f2)*f1,use_unicode=False)
        
        print("Obtenemos:")
        pprint(simplify(diff(f1)*f2+diff(f2)*f1),use_unicode=False)
        return simplify(diff(f))
    else:
        print("Revisa tus entradas, algo salio mal.")
        derivaciondeproducto(f)

Regla del cociente

$$\left(\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-g'(x)f(x)}{\left[g(x)\right]^2}$$

Ya que no siempre se tienen productos entre las funciones, es necesario entender como derivar una división, por ejemplo $$h(x)=\frac{3x+1}{e^{2x+6}}$$ su derivada será $$h'(x)=\frac{(3+0)e^{2x+6}-e^{2x+6}(2)(3x+1)}{\left[e^{2x+6}\right]^2}=\frac{3e^{2x+6}-e^{2x+6}(6x+2)}{\left[e^{2x+6}\right]^2}=\frac{-6x+1}{e^{2x+6}}$$

Igual que en el ejemplo anterior haremos un algoritmo simple que permita recosntruir el procedimiento que calcula la derivada de un cociente:

def derivaciondecociente(f):
    print("Identifique dos posibles factores de") 
    pprint(f,use_unicode=False) 
    
    f1=input("Ingrese el numerador: ")
    f1=sympify(f1)
    f2=input("Ingrese el denominador: ")
    f2=sympify(f2)
    if simplify(f1/f2)==simplify(f):
        print("Muy bien. El calculo de la derivada se hace de la siguiente manera:")
        pprint((diff(f1)*f2-diff(f2)*f1)/(f2**2),use_unicode=False)
        
        print("Obtenemos:")
        pprint(simplify((diff(f1)*f2-diff(f2)*f1)/(f2**2)),use_unicode=False)
        return simplify(diff(f))
    else:
        print("Revisa tus entradas, algo salio mal.")
        derivaciondecociente(f)

Ejercicio

Ejecute las siguientes celdas y describa que se está haciendo cada una. Explique que hace la función prod() y divi().

f=E**x

g=(4*x-5)**3

diff(g*f)

$\displaystyle \left(4 x - 5\right)^{3} e^{x} + 12 \left(4 x - 5\right)^{2} e^{x}$

h=3*x+1

j=E**(2*x+6)

diff(h/j)

$\displaystyle - 2 \left(3 x + 1\right) e^{- 2 x - 6} + 3 e^{- 2 x - 6}$

def prod(f,g):
    return diff(f)*g+diff(g)*f

prod(f,g)

$\displaystyle \left(4 x - 5\right)^{3} e^{x} + 12 \left(4 x - 5\right)^{2} e^{x}$

def divi(f,g):
    return (diff(f)*g-diff(g)*f)/(g**2)

divi(h,j)

$\displaystyle \left(- 2 \left(3 x + 1\right) e^{2 x + 6} + 3 e^{2 x + 6}\right) e^{- 4 x - 12}$

Ejercicios

Calcule las derivadas de las siguientes funciones usando derivaciondeproducto() y derivaciondecociente(), NO SE ANGUSTIE si tiene dificultades al ingresar las funciones. Preguntele a su profesor.

1. $x^3e^x$

2. $(x^2+2x+1)(x+\frac{1}{x})$

3. $\cfrac{x^2+3x-1}{\sqrt{x}+3}$

4. $\cfrac{1}{x^2+e^{12x-10}}$

5. $\sqrt[3]{x}\ln x$